Games101 - MVP变换
从三维旋转到欧拉角
首先三维旋转绕某个轴旋转,已经知道是这样的了。
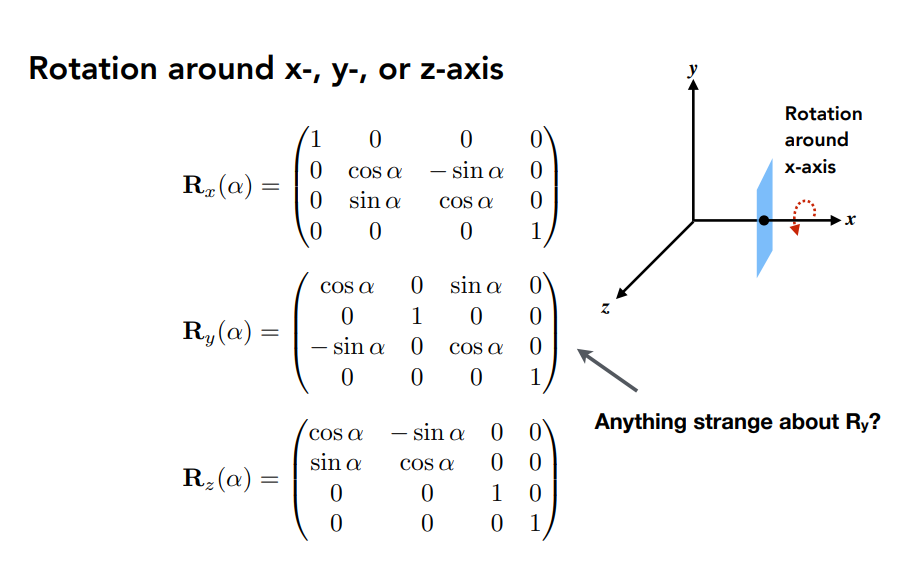
那么就可以通过对3个轴的旋转分别描述,来实现复杂的旋转角。这3个旋转角就叫做欧拉角。
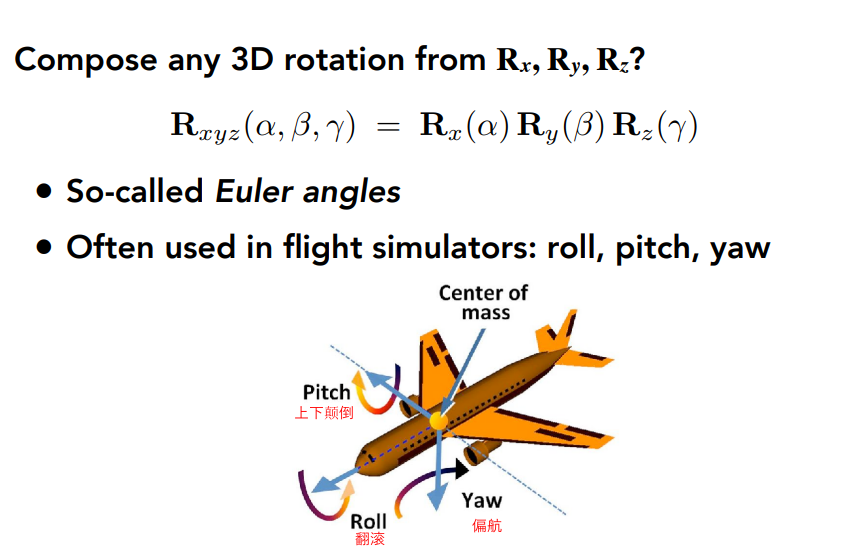
罗德里格斯旋转公式
一个公式,来实现绕轴n旋转α角度。轴n的定义为起点为原点,方向为n。
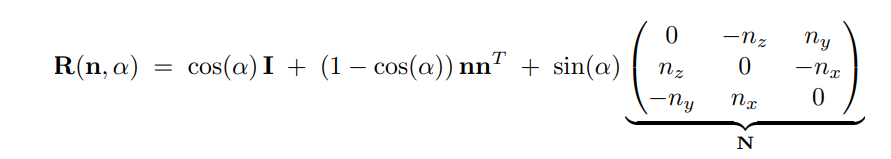
推导
// TODO
四元数的引入
由于用旋转矩阵来做平滑插值并不合理(旋转20°矩阵 和 旋转50°矩阵 的平均值并不是旋转35°),并且存在万向锁问题,所以引入四元数。games101不展开。
MVP变换
Model-View-Projection 模型-视图-投影变换:将3D的模型(Model)投影到2D的屏幕(View)上。
先定义相机的 位置 Position、朝向 Look-at、向上方向 Up direction(与朝向垂直,用于确定相机本身的旋转角)。
视图结果是相对不变的,当物体和相机的移动方式完全一致、没有相对运动时,成像不变。
标准相机
我们定义一个Position在 原点,Look-at在 -Z,Up direction在 Y的相机作为默认相机。
以后就可以将其他相机移成标准相机、然后再做变换、最后移回就实现了相机旋转。
投影 Projection
投影是说3D转到2D屏幕的过程。首先分2种,正交投影和透视投影 Perspective。
正交不会有近大远小、每个平行边也不会有交点,但透视都会有。
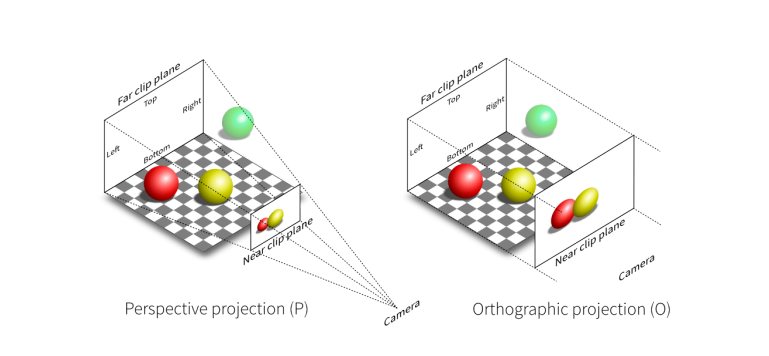
正交投影 Orthographic
定义6个点,就可以描述一个3维的长方体:
x轴:left => right ;y轴:buttom => top ;z轴:fear => near 。
注意z轴,因为上面所有的=>指的都是右手坐标系的负=>正,near离我们更近、被定义为正值。
OpenGL用的是左手坐标系,全部相反。
标准化
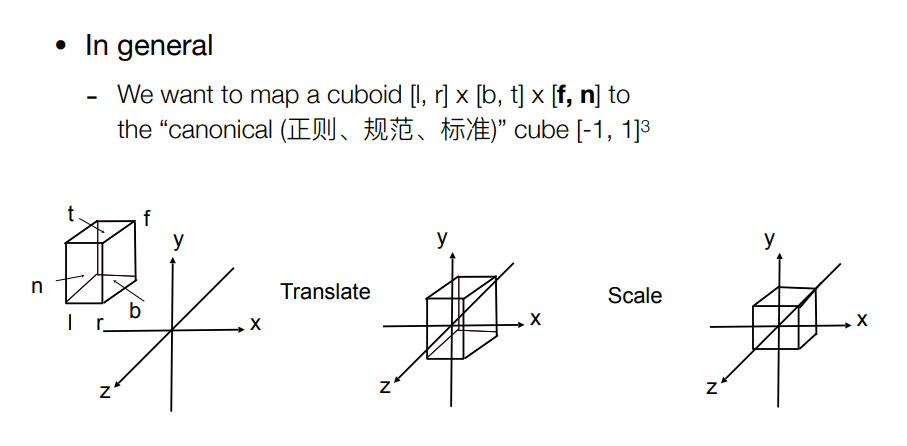
上图的过程就是标准化,也就是将一个长方体变成一个中心点为原点,6个点为-1、1的正方体。标准化的好处是能够更好做正交相机的投影。
标准化的变换矩阵如下,将长度定为2是为了满足(-1,1)。
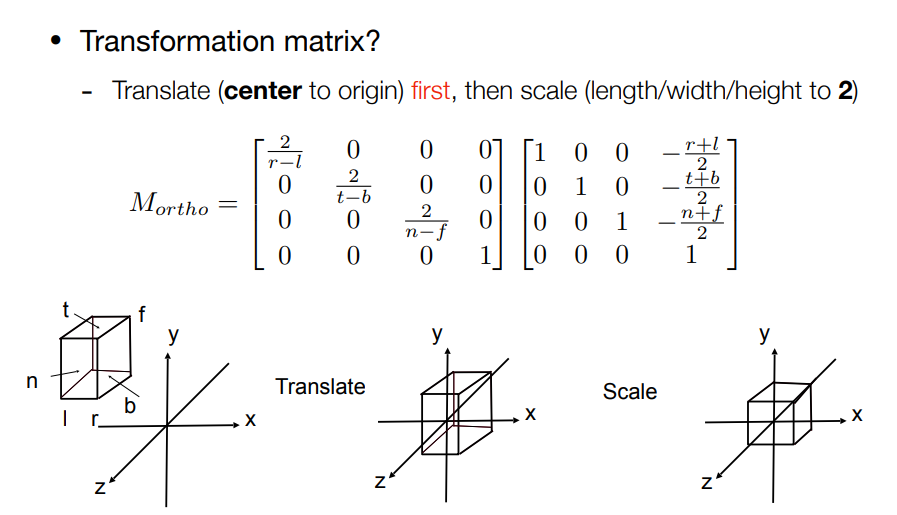
透视投影 Perspective
近大远小、平行线会相交。这是因为不同平面内的线投影到一个平面,会有交点。
齐次坐标性质
(x,y,z,1) 和 (kx,ky,kz,k) 表示的是同一个点。

透视投影拆分⭐
要实现一个透视投影变换,拆成2步:1.将透视投影相机视锥,挤成一个长方体(正交相机视锥);2.将得到的长方体进行正交投影。
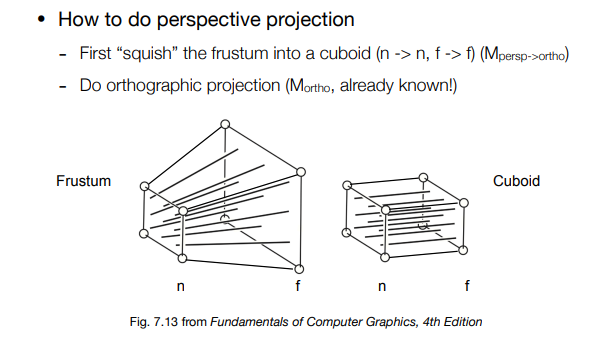
第二步的做法已经在正交投影里写了,那么关键就是第一步怎么做,其实就是乘以一个 透视=>正交 的拉伸矩阵M。
这个矩阵M(4x4)的推导如下:
1.近似三角形可推导出除了第三行以外的所有矩阵
2.性质:近平面点挤压后,点坐标的x,y,z都不变(相机的近平面,就是最终2d屏幕的大小)
3.性质:远平面点挤压后,点坐标的z不变(z轴是深度,想象一下拉伸后,远平面的深度不会变)
4.根据性质2、3可以推导出矩阵的第三行
具体推导看第四章的PPT p29-36吧,这里把主要的近似三角形概念图放下来,结合上面的拉伸概念图可以自己推导了:
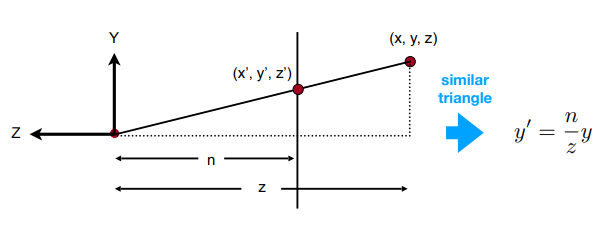
最后4x4的透视=>正交 的拉伸矩阵M:
n 0 0 0
0 n 0 0
0 0 n+f -nf
0 0 1 0

