Games101 - 矩阵变换入门
向量 Vector
小概念
数学上叫做向量,物理上喜欢称作矢量。
向量的模 Magnitude。
向量的归一化,意味着求单位向量 unit Vector。
向量矩阵
下面是在表示笛卡尔坐标系x-y下的某个向量,可以用矩阵来表示向量。
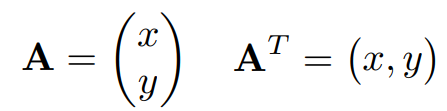
点乘 Dot
满足交换律、结合律、分配律。
结果是一个数值,可以用来检测2个向量的夹角,<90度为正,90度为0,90~180度为负。
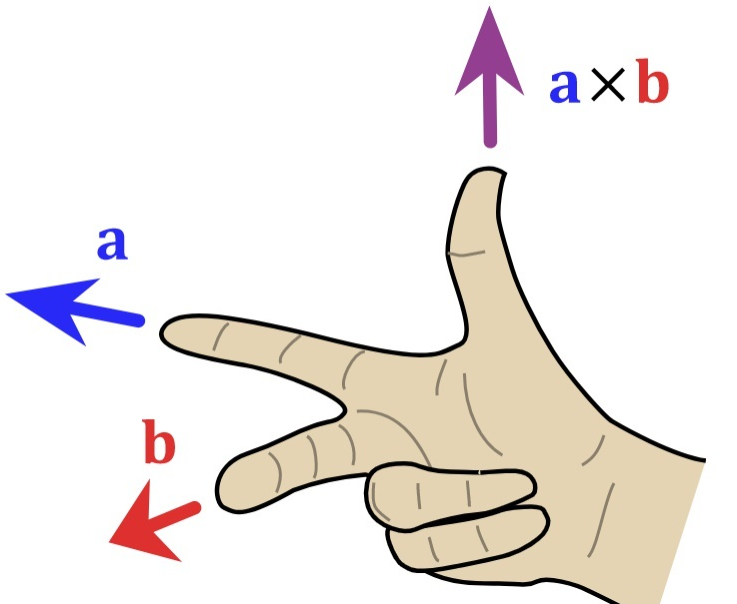
叉乘 Cross
不满足交换律!向量A x 向量B = -向量B x 向量A
结果是一个向量,这个向量是与A、B向量所组成平面的垂直向量,也就是说A、B、C向量构成一个右手直角坐标系。而法线的方向,满足右手螺旋。注意a在前所以a是食指。
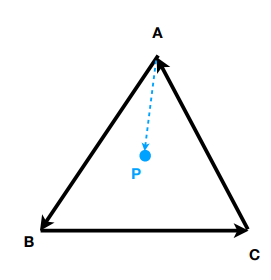
图形学上,用来检测某个点是否在一个多边形(比如三角形)内。
//因为 向量AB x 向量AP 的结果大于0则说明P在AB左侧,小于0则说明P在AB右侧。
更新=> 首先确定是左手还是右手坐标系。在【右手坐标系】下,如果两个向量的叉乘结果为正值,表示向量AB经过不大于180°的【逆时针】旋转可以与向量AP的方向一致;如果为负,那么就需要转180°到360°(右手法则)。
至于为什么,思考一下a X b = |a|*|b|*sinθ,其中sin的值范围是0°-180°为正,180°-360°为负,就可以知道了。点乘几何意义也是同理,靠cos的值判断的。
所以一个三角面ABC和一个点P,只要通过3次叉乘的结果(都大于0或者都小于0),就能判断出点P在三角面ABC中。这是光栅化的基础,用于着色判断。
矩阵变换:线性变换
关键是,要找出变换前后每一个点之间的变化关系式。矩阵的乘法是不满足交换律的。
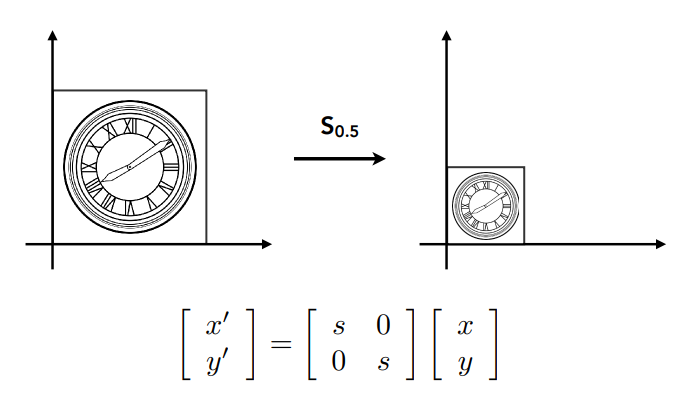
缩放 Sacle
可以使用对角阵*向量来进行缩放,这个对角阵叫缩放矩阵。
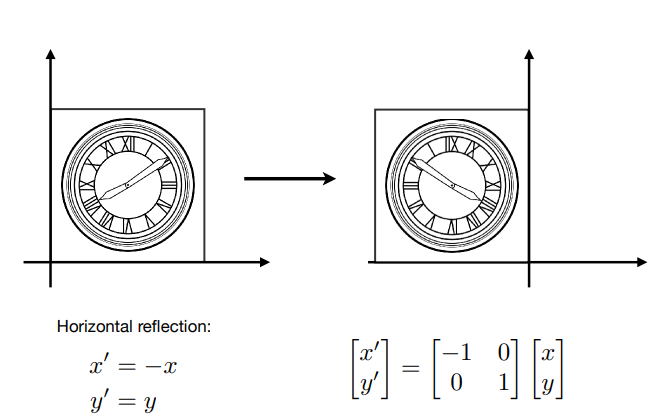
反射 Reflection
用于翻折的单位矩阵。
切变 Shear
要找出每一个点之间的变化关系式。
比如下图情况,只是水平方向的点发生了变化,竖直方向的不变。水平方向上的每个点发生了a / 1 * y的平移。那么久可以很容易写出切变矩阵。

旋转 Rotate
二维情况下,逆时针旋转θ角:
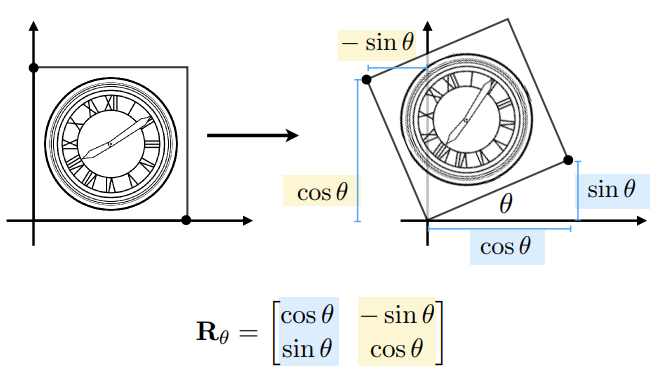
推导过程(只展示A、C。B、D的话由点0,1可以推出)如下,其实只是展开了点(1,0)的偏移等式。
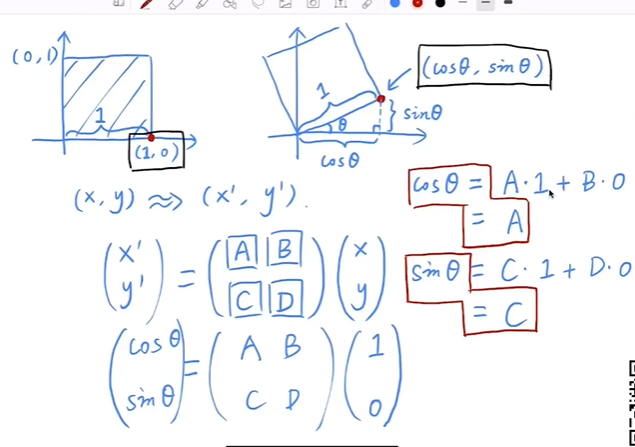
再进一步探究可知,逆旋转矩阵 = 将原旋转矩阵转置。这意味着想要旋转一个负角度,只要求出正角度的旋转矩阵再转置就可以得到旋转矩阵了。
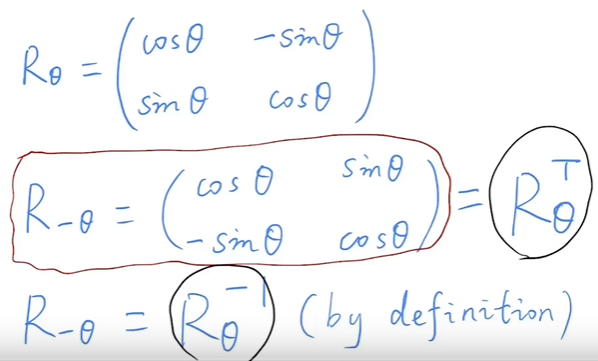
统称:线性变换
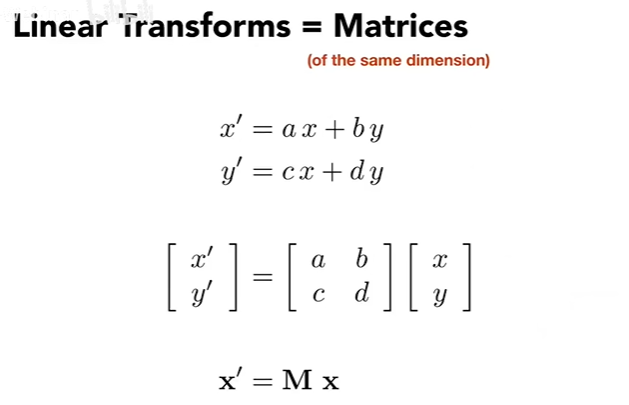
矩阵变换:非线性变换
平移 Translation
平移比较特殊,它不能通过2阶矩阵线性变换(矩阵乘法)得出。因为矩阵乘法你只能得到ax+by的结果,没法出现常数c,所以只能靠加法。
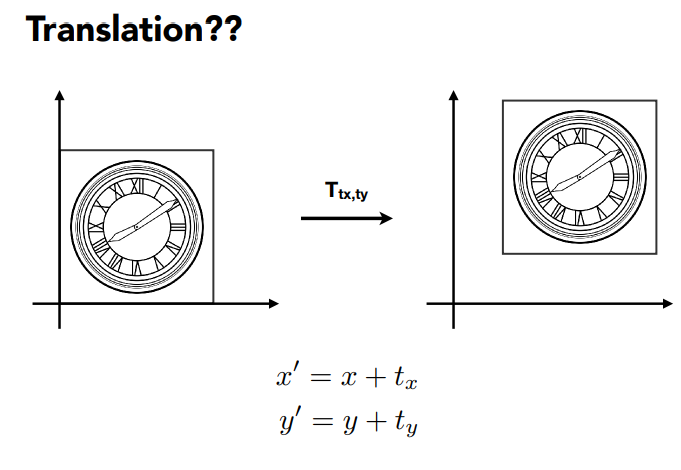
平移解决方案:更高1阶的矩阵
平移必须涉及到同阶矩阵的加法,没法直接用线性变换了。为了在这种情况下也能只使用矩阵乘法就达到变换的目的,可以使用2+1阶的矩阵。多出来的矩阵值,点是1、向量是0。

将二维的点,最后一个矩阵值写为1。如果不是1,那么就看作x => x/w、y => y/w。

那么最后,给出2维 向量、点 的变化矩阵:

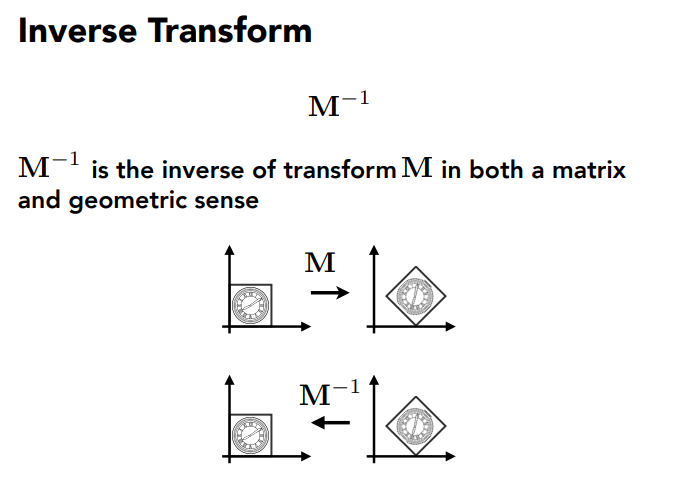
逆变换 Inverse
通过使用逆矩阵,可以撤回变换。
组合的矩阵变换
先旋转,后平移。否则会出错,因为矩阵乘法没有交换律!
那么通过矩阵乘法表示线性变换、矩阵平移的时候,就是从右到左一个个乘。

虽然没有交换律,但是有结合律,可以让前面的变换矩阵合成为一个:

分解复杂的矩阵变换
对于一个复杂的矩阵变换(线性变换+平移变换),需要分解为几步,才能通过矩阵乘法来实现。
绕某点旋转
将c移到原点 => 绕原点旋转 => 移回原来
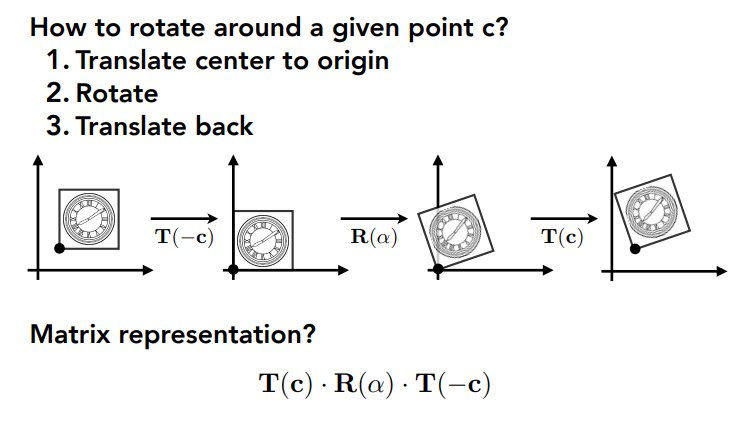
由二维引申到三维
上面讨论的都是二维,转到三维空间,其实也是一样的。

三维缩放、平移
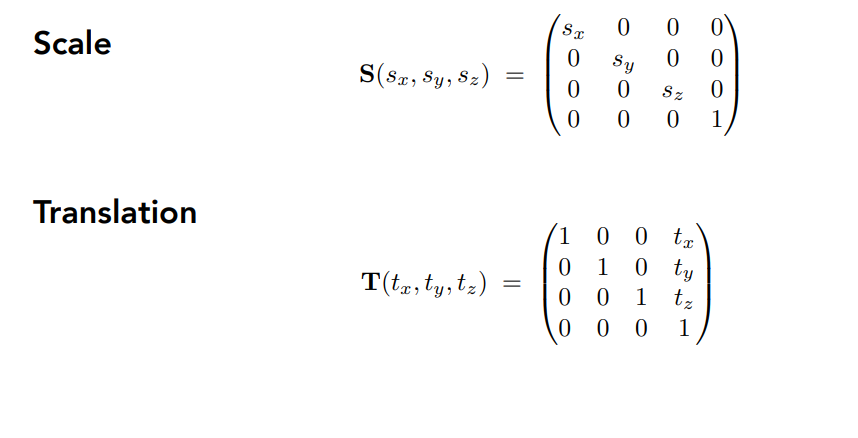
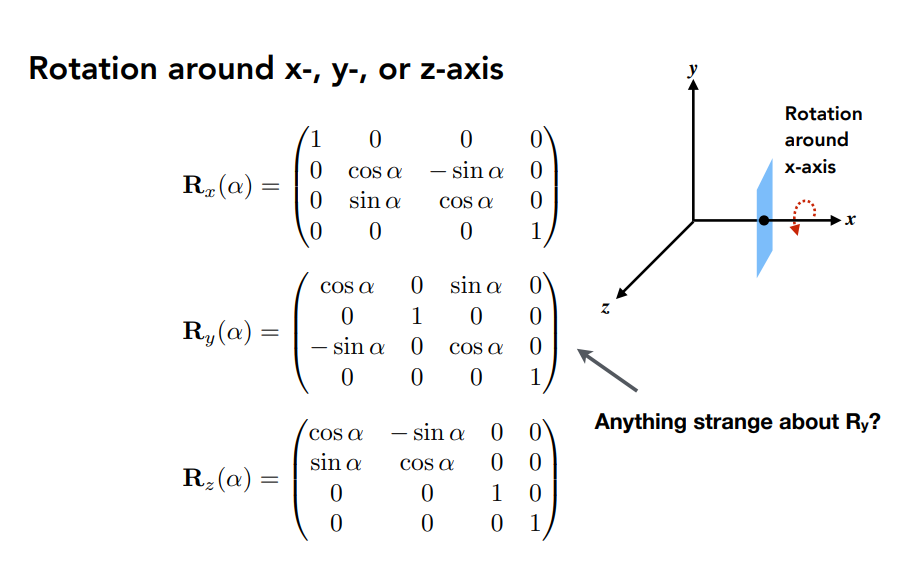
三维旋转
绕某个轴旋转,该轴上的点位置不变。
至于为什么y和x、z轴旋转不一样,详细参考叉乘的右手螺旋定则。