背包问题
基础01背包
问题概述
n种物品每种只有1个。
每个物品有自己的weight和value,求解一个MAX_Weight的容量的背包尽可能多装value的解法。
暴力法
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
背包MAX重量为4。
每个物品只有2个状态(0或1),直接用回溯算法进行枚举。解决本题的时间复杂度为O(2^n) = 8。
动态规划法
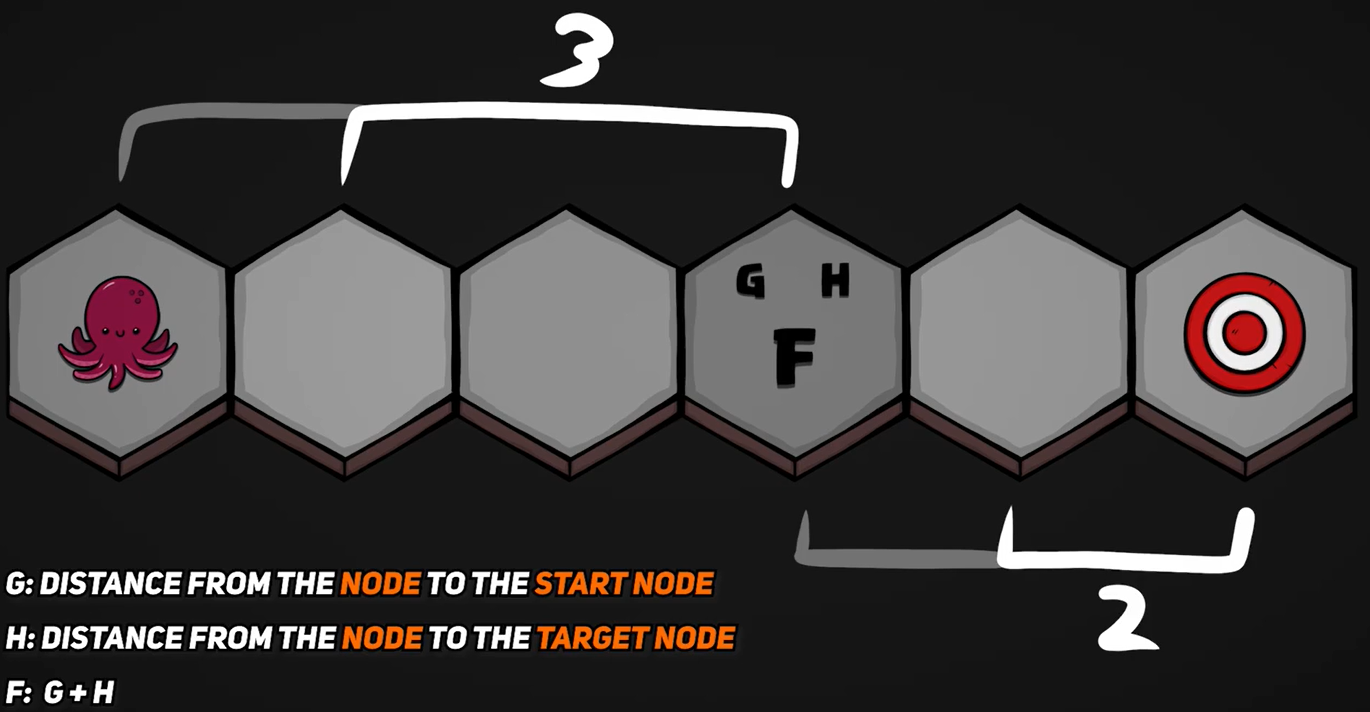
dp数组
一个二维数组,
下标i 对应条件0~i 的物品任取,下标j 对应背包重量。
dp[i][j] 的值 对应 当0~i的物品任取、一个容量为j的背包所放物品的最大value。
递推公式
考虑一个dp[i][j]的前后。
首先dp[i][j]前面说过,代表i、j情况下的最大value,
那么不放物品i的最大价值:dp[i-1][j](不考虑放入物品i但保持j背包重量的情况下的最大价值)
从而推出放物品i的最大价值:dp[i-1][j-weight[i]] + value[i](一定放物品i的背包的最大价值)
从上面的递进关系可以推出公式,dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i]) ;
dp数组初始化
利用推出的公式dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i]) ;

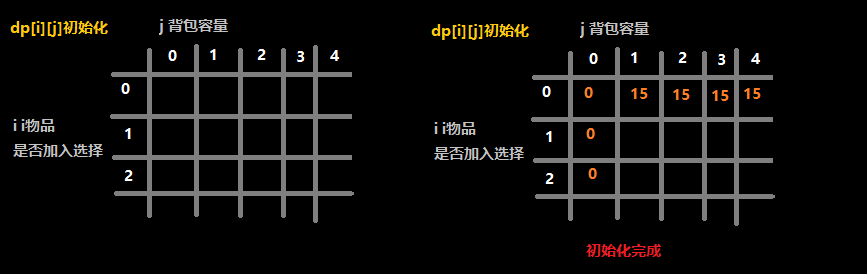
因为所有的数据都是 max(正上方数据,左上角某一个数据 + value[i])。所以初始化只要把第一行和第一列正确初始化,其他的都可以靠递推公式推出。
第一列因为背包容量为0所以固定全是0,而第一行很容易计算。
最后初始化完成结果如图:
遍历顺序
二维dp数组其实都可以(因为确定数值时左上方的数值都已确定),但是常规选择:
1 | for(物品) |
解题案例
题目还是前面的那个题目。手写一遍,再代码实现一遍。
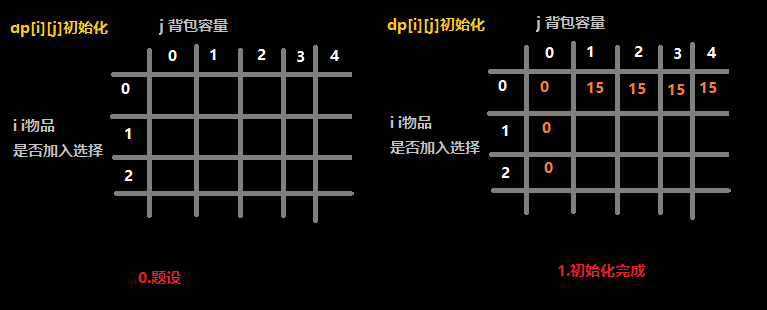
动态规划手写
不说了…图画了我半小时…
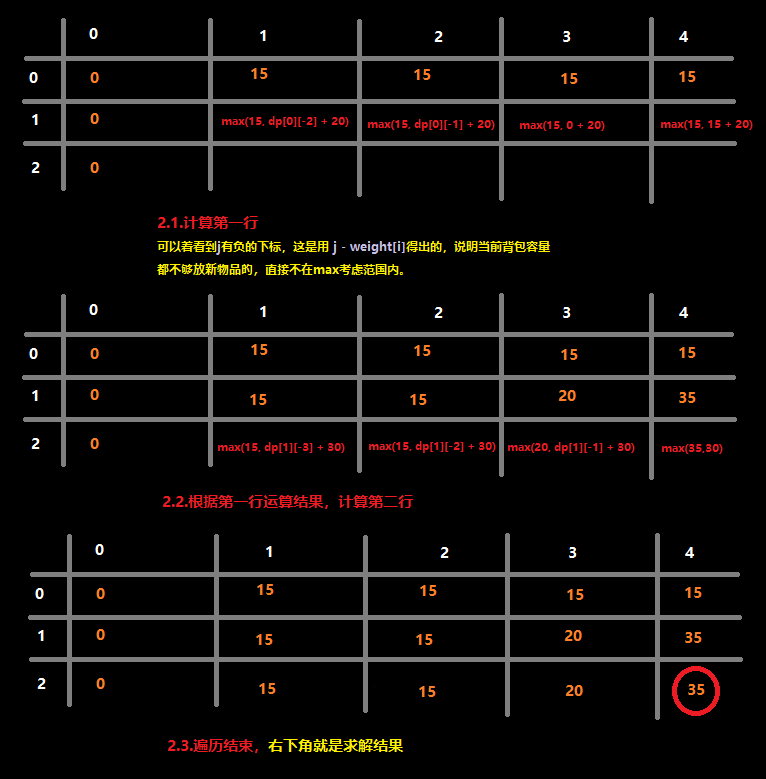
代码实现
完全背包
问题概述
n种物品每种有无限个。
多重背包
问题概述
n种物品每种物品个数各不相同。