初识

什么是定点数？

约定计算机中小数点的位置，且这个位置固定不变，小数点前、后的数字，分别用二进制表示，然后组合起来就可以把这个数字在计算机中存储起来，这种表示方式叫做「定点」表示法，用这种方法表示的数字叫做「定点数」。

为什么不用浮点数？

具体怎么使用？

定点数参与逻辑运算，转换回浮点数后不再用浮点数参与任何逻辑运算。

定点数型Int

从浮点数转换到定点数

放大1024倍，从而使得浮点数小数误差变小。

用long存储防止高位越界。

使用移位运算实现，比直接乘更优。

int型转换可以不损失精度；float型转换需要损失一些精度：(long)Math.Round(f * 1024)。

乘除运算出现问题

乘法运算相当于多乘了一次倍数，所以直接除以1024（右移10位）即可。1024(原数1) * 2048(原数2) = 2^21 (原数是2^11而不是期待的2)

除法运算相当于多除了一次倍数，所以直接乘以1024（左移10位）即可。2048(原数2) / 1024(原数1)= 2 (原数是2^-9而不是期待的2)

大小比较

简单重写operator。

定点数转换回浮点数

缩小1024倍之后强转float，右移10位强转int。但这样会导致负数位移出现问题，见下。

位移运算问题

在计算机中，负数使用二进制补码表示。原因是方便直接进行逻辑电路（与非门）运算，把减法直接变成加法。比如-3 1 011的补码是1 101，那么实现3-3就是0 011 + 1 101刚好意味着0 000。

而.net的位移运算用的是算数位移，比如对int或long进行右位移时，如果左侧符号位为非负(0)，高位补0；如果左侧操作数为负(1)，高位补1。

以上2点就导致，c#中int型和long型的正数和负数的位移是不对等的，也就是两者位移完的非符号位原码不一样！

比如

0 011(3)右位移1次 => 0 001 = 0 001(原码) = 1;

1 101(-3以补码形式出现)右位移1次 => 1 110 = 1 010(原码) = -2;

都是右移一位，一个是1，一个是-2而不是-1，这就叫不对等。

解决方案在理解原理之后就很简单：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private const int BIT_MOVE_COUNT = 10;
public int RawInt
{
    get
    {
        if (scaledValue >= 0)
        {
            return (int)(scaledValue >> BIT_MOVE_COUNT);
        }
        else
        {
            return -(int)(-scaledValue >> BIT_MOVE_COUNT);
        }
    }
}

定点向量Vector3

用上面实现的 定点数型Int 来实现一个Vectors：

  • 定点数Int型的xyz值
  • 索引、操作数
  • 常用向量定义
  • 与UnityEngine.Vector3的转换
  • 求向量长度平方 与 向量的长度也就是模（取平方根）
  • 规格化（1/向量的模 * 向量）
  • 点乘、叉乘、夹角

其中，计算向量长度（模）需要自己实现取定点数的平方根，使用牛顿迭代法求平方根。简单来说就是通过多次迭代求接近于平方根的数据。

而计算夹角也需要用到反余弦值，所以要自己实现定点数求反余弦函数。

下面对两者详解：

牛顿迭代法优化

求模公式|a|=√(x^2+y^2+z^2），需要实现定点数平方根。原理部分如下，这里感谢Plane大神提供的笔记和思路！

优化因为比较简单，直接上代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int iteratorCount = 8;// 默认迭代8次
===================================================================================

// 优化前：
for (int i = 0; i < iteratorCount;i ++)
{
    result = (result + val / result) >> 1;
}

// 虽然默认迭代8次，但是可能因为数值原因导致有的不需要8次就已经很接近了，优化点就在这
// 优化后：
do
{
    history = result;
    result = (result + val / result) >> 1;
    ++count;
}
while (result != history && count < iteratorCount);

点乘叉乘

https://zhuanlan.zhihu.com/p/359975221

除此之外，补充一下，我个人的理解：

首先确定是左手还是右手坐标系。在【右手坐标系】下，如果两个向量的叉乘结果为正值，表示向量a经过不大于180°的【逆时针】旋转可以与向量b的方向一致；如果为负，那么就需要转180°到360°（右手法则）。

至于为什么，思考一下a X b = |a|*|b|*sinθ，其中sin的值范围是0°-180°为正，180°-360°为负，就可以知道了。点乘几何意义也是同理，靠cos的值判断的。

夹角

向量夹角使用公式：

也就是说实现向量的 点乘运算、求模运算、反余弦函数，就可以由2个向量计算出夹角了。

点乘、求模（牛顿法）上面已实现。夹角需要自己实现求反余弦函数，实现方法如下。

反余弦值分割成一张表

直接通过枚举1024份对应的x-y数值来获得，而作为结果的反余弦函数的弧度制的值[0,π] 则通过小数值放大10000倍取整。

原理部分如下原理部分如下，这里感谢Plane大神提供的笔记和思路！

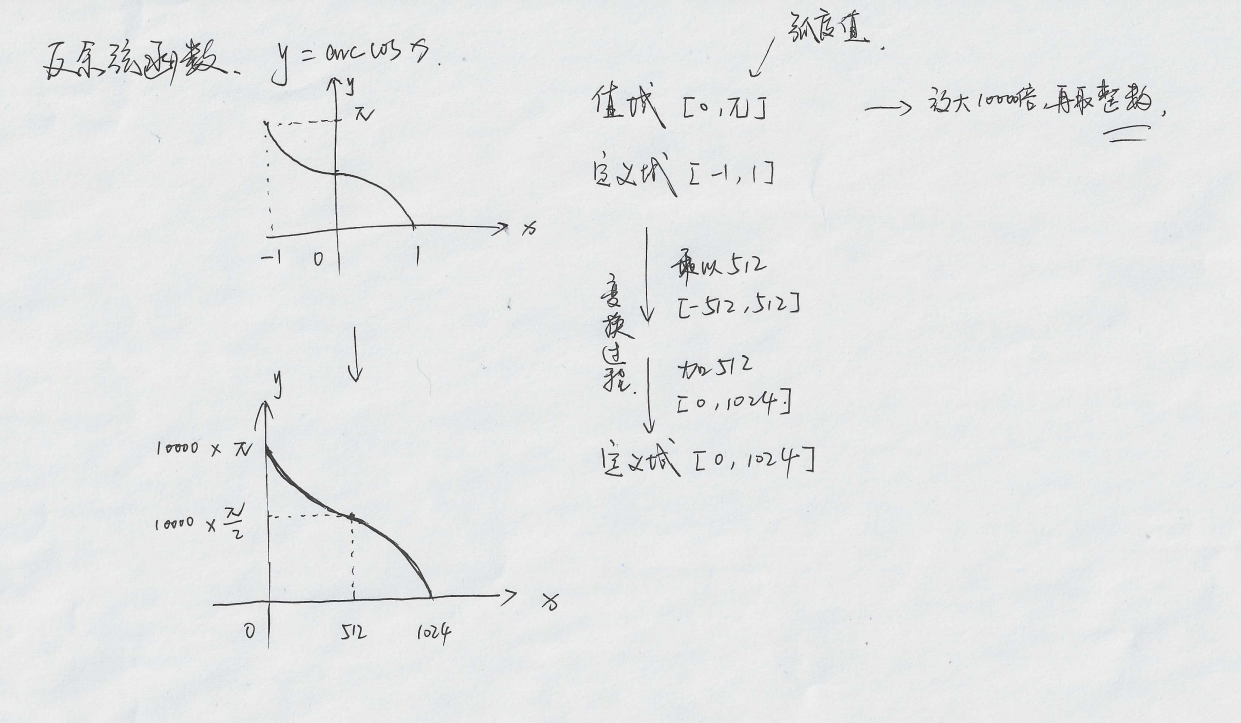
级数映射查表

上面提到的枚举1024份的反余弦函数弧度制的值，就是一张有1025个数值（分割成1024份就有1025个点）的表，需要用级数查到对应的表值。

根据公式，x就是向量积/模。所以映射也就是将 [-1,1] 映射成 [0,1024]。

1
2
3
4
5
6
7
8
9
// 求反余弦。val就是向量积/模，范围是[-1,1]
public static CodingKArgs Acos(CodingKInt val)
{
    CodingKInt rate = (val * AcosTable.HalfIndexCount) + AcosTable.HalfIndexCount; // 将 [-1,1] 映射成 [0,1024]
    rate = Clamp(rate, CodingKInt.zero, AcosTable.IndexCount);// 限制rate范围为 0 ~ 1024
    int rad = AcosTable.table[rate.RawInt];// 查表

    return new CodingKArgs(rad, AcosTable.Multipler);// 返回查表结果（弧度值）
}