A*算法

A*算法是什么

原理

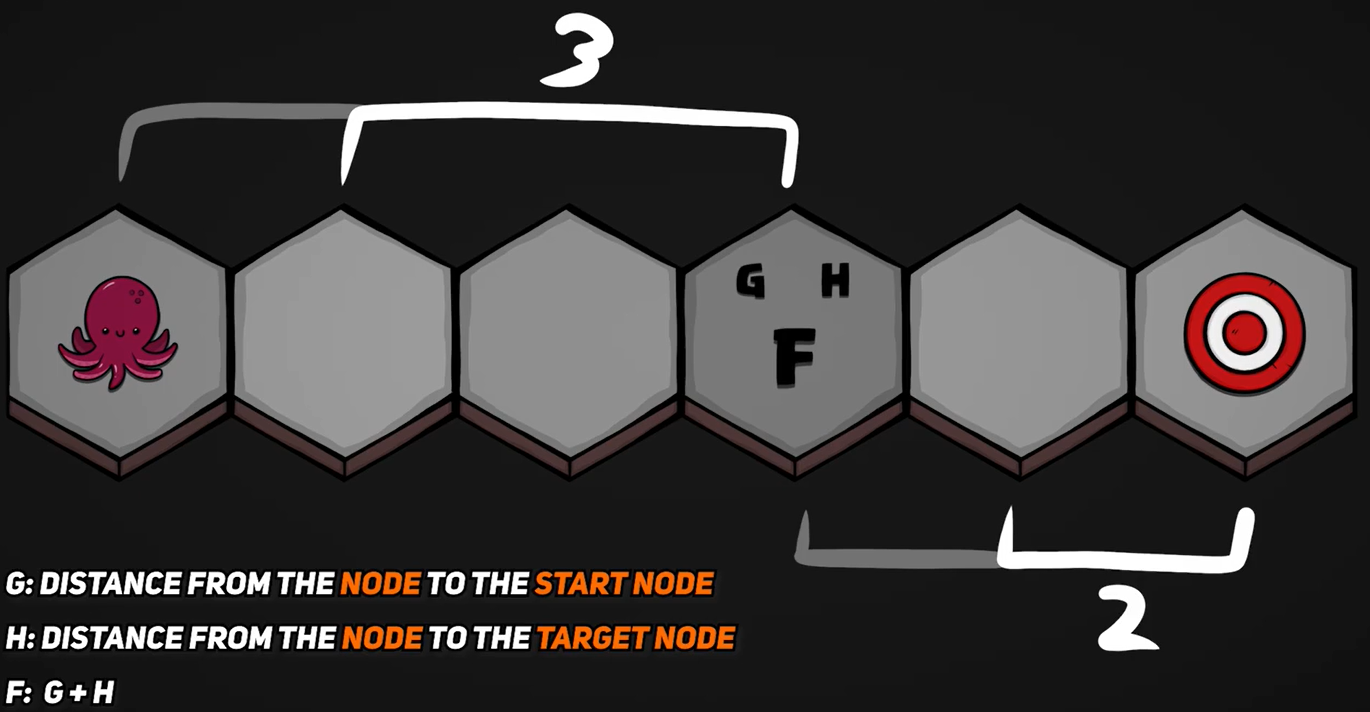
主要利用到3个数值，

  • G Cost：从出发点到该点已花费的距离。
  • H Cost：从该点到终点的最乐观距离（不考虑障碍等因素）。
  • F Cost = G Cost + H Cost，它越低，作为寻径选择就越有吸引力。

目标是简单选择最低的F Cost，一步一步往后踩，每一步都记录附近没踩过的格子的F Cost到列表里。每踩下去一步后，如果发现周围邻近的格子F Cost都比过去的某个列表里的格子的F Cost大，就用那个列表里的格子继续踩。

不断重复，直到我们到达目标节点。

NodeBase

1
2
3
4
5
6
7
8
9
10
11
12
13
public class Nodebase {
	public float G { get; private set; }  
	public float H { get; private set; } 
	public float F => G+H
        
    public Nodebase Connection { get; private set } 
    public List<NodeBase> Neighbors { get; protected set; }
    
	public void Setconnection(Nodebase nodebase) => { Connection = nodebase; }
    public float GetDistance(NodeBase other) => Coords.GetDistance(other.Coords); // reduce noise,优化的话主要就优化这里
	public void SetG(float g) => G=g
	public void SetH(float h) => H=h;
}

算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
public static List<NodeBase> FindPath(NodeBase startNode, NodeBase targetNode)
{
	// 接下来需要探索的结点。又名“开放列表”。
	var toSearch = new List<NodeBase>() { startNode };
	// 已处理过的结点：一旦进入该队列，就再也不会更新结点值、探索了。又名“关闭列表”。
	var processed = new List<NodeBase>();

	while (toSearch.Any())
	{
		var current = toSearch[0];
		foreach (var t in toSearch)
        {
            // 0.获取一个【乐观总长F】最好的结点，或者F相同但是【乐观H】最好的结点
            if (t.F < current.F || t.F == current.F && t.H < current.H) current = t;
        }

		// 1.将此结点作为探测完毕的结点
		processed.Add(current);
		toSearch.Remove(current);
		current.SetColor(ClosedColor);

		// 2.探测是否是终点结点
		if (current == targetNode)
		{
			var currentPathTile = targetNode;
			var path = new List<NodeBase>();
			var count = 100;
			while (currentPathTile != startNode)
			{
				path.Add(currentPathTile);
				currentPathTile = currentPathTile.Connection;
				count--;
				if (count < 0) throw new Exception();
				Debug.Log("sdfsdf");
			}

			foreach (var tile in path) tile.SetColor(PathColor);
			startNode.SetColor(PathColor);
			Debug.Log(path.Count);
			return path;
		}

		// 3.将该结点的所有邻居结点进行更新(只更新未被加入已处理队列的)
		foreach (var neighbor in current.Neighbors.Where(t => t.Walkable && !processed.Contains(t)))
		{
			// ① 如果该邻居不在未来需要探索的结点队列中
			var inSearch = toSearch.Contains(neighbor);
			// ② 如果该邻居的开销G > 本结点开销G + 本结点到该邻居距离
			var costToNeighbor = current.G + current.GetDistance(neighbor);
			// ① || ②
			if (!inSearch || costToNeighbor < neighbor.G)
			{
				// ③ 根据当前结点的【开销G】，更新所有邻居的G和路线为目前最优解。
				neighbor.SetG(costToNeighbor);
				neighbor.SetConnection(current);

				if (!inSearch)
				{
					// ④ 如果更新了的数据结点不在探索队列，就更新它的【乐观H】，并将其加入探索队列
					neighbor.SetH(neighbor.GetDistance(targetNode));
					toSearch.Add(neighbor);
					neighbor.SetColor(OpenColor);
				}
			}
		}
	}
	return null;
}


// 我们确定这个新邻居G Cost的值，然后如果它不在搜索列表中，或者这个G值比现在的G值好，那就设置它的Connection，并更新它的G值

public override void CacheNeighbors() {
    Neighbors = GridManager.Instance.Tiles.Where(t => Coords.GetDistance(t.Value.Coords) == 1).Select(t=>t.Value).ToList();
}

思考

  1. GetDistance是优化的重点，想减少噪音，如何根据具体业务选择最好的算法是值得思考的。
  2. 算法核心就是上面代码的3.这一块：每走一步当前最优时需要更新所有的未探索邻居结点，从中找出更优解作为继续探索的起点。

多种寻路对比

方格版本

1.先做一个地图生成器，每个方格都带坐标，提前生成好地图和每个结点的邻居list；

2.规定横竖都是1长度，斜向是1.4长度(1/cos45°)；

3.有2个列表，一个是【已探索的结点】列表，一个是【即将探索的结点】队列。每一步探索，就是去遍历第二个队列，把里面的结点移到第一个列表里，同时把这个结点的邻居list全部扔到第二个队列里（如果已经在第一个、第二个列表中有，就不扔）。// 这一步是优化点

可以优化的寻路算法

1.宽度优先算法：这个是最简单直白的版本，总体是绕圈方式一点点遍历全图，个体之间是找找到可达就确定一个路径，不进行任何大小比较。这种寻路算法并没有什么意义，效率低且无法找到最短路径，找到的第一个解不一定是最短距离。

2.迪杰斯特拉算法：基于宽度优先算法，总体是绕圈方式，但是个体之间不再是可达就确定，而是不停更新比较、更新成最小值。可以找到最短路径，但是计算量极大，因为需要遍历完整个地图结点才能确定出最短解，不然。

3.贪心算法：追求局部最优解，总体是几乎直线的形式。但是因为走的是局部最优，获得的解在有障碍物的情况下不一定是最优解。速度极快，只能用于中途无障碍的寻路，比如mmo广场。

4.A星算法：结合迪杰斯特拉往后看、贪心往前看，一种综合评估的算法。也会和贪心算法一样选错路，但是很快会调转回头，最终一定能得到一个最短解。

引入优先队列优化

通过引入优先队列，可以解决迪杰斯特拉算法因为无法确定退出时间点，所以需要遍历完全图才能确定获得最短解，导致效率低下的问题。

迪杰斯特拉算法：具体引入就是修改【即将探索的结点】队列，对于每一个priority = 到当前点的最短距离 G Cost，优先去探索最小的sumDistance的点，这样第一个找到的路径就是最短路径。

贪心算法：把上面的priority改为priority = 当前点的乐观最短距离 H Cost。不过这不一定能得到最短解。

A星算法：把上面的priority改为priority = 到当前点的最短距离 G Cost + 当前点的乐观最短距离 H Cost。一定能找到最短解，且性能适中。